DISTRIBUIÇÕES DISCRETAS
\(P(A) = p \) (sucesso)
\(P(\bar{A}) = 1 - p = q \) (insucesso)
X é o número de sucessos em N provas repetidas. $$\sum_{x=0}^{N}f(x) = \sum_{x=0}^{N} \left(\!\begin{array}{c} N \\ x\end{array}\!\right) p^x q^{N-x} =1$$ Quando N=1 temos a distribuição de Bernoulli \(X \sim B(N,p) \) $$f(x|p) =P(X=x) = p^x q^{1-x}, x = 0,1 \; e \; 0 \lt p \lt 1 $$ Consideremos, por exemplo, cinco lançamentos de um dado "perfeito". Qual a probabilidade de se obter duas vezes a face com seis pintas?
Neste caso, \(A\) é o acontecimento saída de seis pintas (sucesso) e \( \bar{A}\) o acontecimento contrário (insucesso). Por conseguinte:
\(p = P(A) = \frac{1}{6}\),
\(q = P(\bar{A})=1-p=\frac{5}{6}\),
\(f(2|\frac{1}{6}) =P(X=2) = \left(\!\begin{array}{c} 5 \\ 2\end{array}\!\right) (\frac{1}{6})^2 (\frac{5}{6})^{3} = 10\times (\frac{1}{6})^2 (\frac{5}{6})^{3} = 0,16\)
Saída de dois 6 em cinco lançamentos
\(AA \bar{A} \bar{A} \bar{A}; A \bar{A}A \bar{A} \bar{A}; A \bar{A} \bar{A} A\bar{A}; A \bar{A} \bar{A} \bar{A}A; \bar{A} AA \bar{A} \bar{A}; \)
\(\bar{A} A \bar{A}A \bar{A}; \bar{A} A \bar{A} \bar{A}A; \bar{A} \bar{A} AA \bar{A}; \bar{A} \bar{A} A \bar{A}A; \bar{A} \bar{A} \bar{A} AA \;\;\;\; \frac{5!}{2!3!}=10\)
\(Mp+Mq = M\)
\(p+q=1\) e \(0 \lt p \lt 1\)
\(E(X) = Np\) e \(V(X) = Npq \frac{(N-M)}{(M-1)} \)
Uma variável aleatória X, com função probabilidade $$f(x) =P(X=x) = \frac{e^{-\lambda }\lambda ^x}{x!}, x = 0,1,2,... \;e\; \lambda \gt 0 $$ diz-se que tem distribuição de Poisson com parâmetro \( \lambda \),
\(X \sim P(\lambda)\) com \(E(X)=\lambda\) e \(V(X) = \lambda\).
A distribuição de Poisson é um caso particular da distribuição Binomial em que \(E(X)=Np=\lambda\) quando \(n \to \infty \Rightarrow p \to 0\) a distribuição Binomial converge para a de Poisson.
5. A distribuição Normal
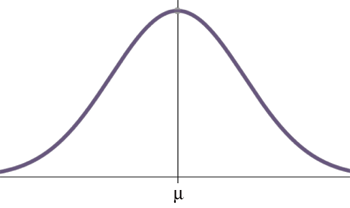
Uma variável aleatória X com função densidade de probabilidade $$f(x)= \frac{1}{{\sigma \sqrt {2\pi } }}e^{{{ - \left( {x - \mu } \right)^2 } \mathord{\left/ {\vphantom {{ - \left( {x - \mu } \right)^2 } {2\sigma ^2 }}} \right.}{2\sigma ^2 } }}$$ diz-se que tem distribuição Normal com parâmetros \(\mu\) e \(\sigma\). Ou seja, \(X \sim \mathcal{N} (\mu,\sigma)\) \((ou,\sigma^2)\) em que \(E(X)=\mu, V(X)=\sigma^2\).
Se \(X \sim \mathcal{N} (\mu,\sigma)\) então a variável \(Z=\displaystyle\frac{X-\mu}{\sigma}\sim N(0,1)\).
E por conseguinte $$f(z)= \frac{1}{{\sqrt {2\pi } }}e^{{{ - z^2 } \mathord{\left/ \right.{2} }}}$$ $$F(z)= \frac{1}{\sqrt {2\pi } } \int_{-\infty}^z e^{{{ - x^2 } \mathord{\left/ \right.{2} }}}dz$$
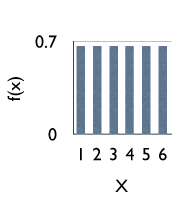
1. A distribuição uniforme $$f(x_i) = P(X=x_i) =\frac{1}{N}, i = 1, 2, ..., N$$ $$E(X) = \frac{1}{N} \sum_{i=1}^{N}x_i \; e \; V(X) = \frac{1}{N} \sum_{i=1}^{N}x_i^2-\left [\frac{1}{N}\sum_{i=1}^{N}x_i \right]$$
Esta função representa experiências como o lançamento de um dado (N = 6) e portanto \(f(x) = \frac{1}{6} \), para x = 1, 2, ...,6. Em termos gráficos temos

2. A distribuição binomial $$f(x|p) =P(X=x) = \left(\!\begin{array}{c} N \\ x\end{array}\!\right) p^x q^{N-x}, x = 0,1,2, ...,N \; e \; 0 \lt p \lt 1 $$ Diz-se então que X segue uma distribuição binomial, \(X \sim B(N,p) \) com \(E(X) = Np\) e \(V(X) = Npq \). Modelo probabilístico adequado para descrever os processos em que se realizam repetidas provas de Bernoulli (sucessões de experiências aleatórias independentes) em que:
\(P(A) = p \) (sucesso)
\(P(\bar{A}) = 1 - p = q \) (insucesso)
X é o número de sucessos em N provas repetidas. $$\sum_{x=0}^{N}f(x) = \sum_{x=0}^{N} \left(\!\begin{array}{c} N \\ x\end{array}\!\right) p^x q^{N-x} =1$$ Quando N=1 temos a distribuição de Bernoulli \(X \sim B(N,p) \) $$f(x|p) =P(X=x) = p^x q^{1-x}, x = 0,1 \; e \; 0 \lt p \lt 1 $$ Consideremos, por exemplo, cinco lançamentos de um dado "perfeito". Qual a probabilidade de se obter duas vezes a face com seis pintas?
Neste caso, \(A\) é o acontecimento saída de seis pintas (sucesso) e \( \bar{A}\) o acontecimento contrário (insucesso). Por conseguinte:
\(p = P(A) = \frac{1}{6}\),
\(q = P(\bar{A})=1-p=\frac{5}{6}\),
\(f(2|\frac{1}{6}) =P(X=2) = \left(\!\begin{array}{c} 5 \\ 2\end{array}\!\right) (\frac{1}{6})^2 (\frac{5}{6})^{3} = 10\times (\frac{1}{6})^2 (\frac{5}{6})^{3} = 0,16\)
Saída de dois 6 em cinco lançamentos
\(AA \bar{A} \bar{A} \bar{A}; A \bar{A}A \bar{A} \bar{A}; A \bar{A} \bar{A} A\bar{A}; A \bar{A} \bar{A} \bar{A}A; \bar{A} AA \bar{A} \bar{A}; \)
\(\bar{A} A \bar{A}A \bar{A}; \bar{A} A \bar{A} \bar{A}A; \bar{A} \bar{A} AA \bar{A}; \bar{A} \bar{A} A \bar{A}A; \bar{A} \bar{A} \bar{A} AA \;\;\;\; \frac{5!}{2!3!}=10\)
3. A distribuição hipergeométrica $$f(x|p) =P(X=x) = \frac{\left(\!\begin{array}{c} Mp \\ x\end{array}\!\right)\left(\!\begin{array}{c} Mq \\ N-x\end{array}\!\right)}{\left(\!\begin{array}{c} M \\ N\end{array}\!\right)}, x = 0,1,2, ...,N \; e \; 0 \lt p \lt 1 $$ Probabilidade de X se, de um universo de M elementos, forem retirados amostras de N elementos sem reposição, onde:
\(Mp+Mq = M\)
\(p+q=1\) e \(0 \lt p \lt 1\)
\(E(X) = Np\) e \(V(X) = Npq \frac{(N-M)}{(M-1)} \)
4. A distribuição de Poisson
Uma variável aleatória X, com função probabilidade $$f(x) =P(X=x) = \frac{e^{-\lambda }\lambda ^x}{x!}, x = 0,1,2,... \;e\; \lambda \gt 0 $$ diz-se que tem distribuição de Poisson com parâmetro \( \lambda \),
\(X \sim P(\lambda)\) com \(E(X)=\lambda\) e \(V(X) = \lambda\).
A distribuição de Poisson é um caso particular da distribuição Binomial em que \(E(X)=Np=\lambda\) quando \(n \to \infty \Rightarrow p \to 0\) a distribuição Binomial converge para a de Poisson.
DISTRIBUIÇÕES CONTÍNUAS
5. A distribuição Normal
Uma variável aleatória X com função densidade de probabilidade $$f(x)= \frac{1}{{\sigma \sqrt {2\pi } }}e^{{{ - \left( {x - \mu } \right)^2 } \mathord{\left/ {\vphantom {{ - \left( {x - \mu } \right)^2 } {2\sigma ^2 }}} \right.}{2\sigma ^2 } }}$$ diz-se que tem distribuição Normal com parâmetros \(\mu\) e \(\sigma\). Ou seja, \(X \sim \mathcal{N} (\mu,\sigma)\) \((ou,\sigma^2)\) em que \(E(X)=\mu, V(X)=\sigma^2\).

Neste contexto e independentemente dos valores concretos de \(\mu\) e \(\sigma\) $$ \int_{-\infty}^{+\infty} \frac{1}{{\sigma \sqrt {2\pi } }}e^{{{ - \left( {x - \mu } \right)^2 } \mathord{\left/ {\vphantom {{ - \left( {x - \mu } \right)^2 } {2\sigma ^2 }}} \right.}{2\sigma ^2 } }}dx = 1$$
A distribuição normal reduzida ou estandartizada
Se \(X \sim \mathcal{N} (\mu,\sigma)\) então a variável \(Z=\displaystyle\frac{X-\mu}{\sigma}\sim N(0,1)\).
E por conseguinte $$f(z)= \frac{1}{{\sqrt {2\pi } }}e^{{{ - z^2 } \mathord{\left/ \right.{2} }}}$$ $$F(z)= \frac{1}{\sqrt {2\pi } } \int_{-\infty}^z e^{{{ - x^2 } \mathord{\left/ \right.{2} }}}dz$$
A Distribuição Normal (a azul) e a Distribuição Normal Reduzida (a vermelho) Mova os pontos vermelhos para calcular \(P(C \leq Z \leq D) \) ou os pontos azuis para \( P(A \leq X \leq B) \).