| ||||
a) Para cada um dos conjuntos de dados calcule: média , mediana, intervalo de variação, desvio padrão e coeficiente de variação.
b) Compare as rendas dos quartos de Lisboa e Faro.
2. Os seguintes dados representam previsões de 25 economistas para o crescimento real do PIB num determinado ano:
| ||||
a) Calcule: média, mediana, moda, intervalo de variação, intervalo interquartis, variância, desvio padrão e coeficiente de variação.
b) Apresente o diagrama \(\textit{stem and leaf}\) e o gráfico \(\textit{box and whisker}\).
c) Refira-se à configuração da distribuição.
3. Num determinado campeonato de futebol foram marcados golos em 320 jogos ao longo da época 2015/2016. O quadro seguinte apresenta a distribuição do número de golos pelo número de jogos. $$ \newcommand\T{\Rule{0pt}{0.25em}} \begin{array}{ c c c c c c c c c c c c } \hline \textbf{Número de golos}& 0 & 1 & 2& 3&4&5&6&7&8&9&10 \\ \textbf{Número de jogos} & 20 & 73 & 88&70&28&20&14&3&2&1&1 \\ \hline \end{array} $$ a) Calcule a média e a variância do número de golos;
b) Represente graficamente a informação publicada no quadro.
4. Numa determinada empresa foi registado o tempo (em minutos) despendido, por cada um dos seus 42 trabalhadores, no percurso entre a respetiva residência e o local de trabalho:
| ||||
Aproxime:
b) A média, a mediana e a moda.
c) O primeiro e o terceiro quartis.
d) O intervalo de variação e o intervalo inter-quartis.
e) A variância, o desvio padrão e o coeficiente de variação.
f) Construa o histograma e o polígono de frequências.
g) Construa o diagrama "box-and-whiskers" e refira-se quanto à configuração da distribuição.
h) Construa o polígono acumulado (ogiva) e assinale os quartis.
i) Quantos trabalhadores gastam até 20 minutos para chegar ao local de trabalho?
j) Quantos trabalhadores gastam mais de 36 minutos para chegar ao local de trabalho?
5. As classificações,numa escala de 0 a 200, obtidas por 300 alunos distribuídos em duas turmas (A e B) são apresentadas na tabela seguinte:
| ||||
a) as medidas de localização;
b) as medidas de dispersão;
Classifique os dados em 5 classes e, com base nesta agregação, aproxime para ambas as turmas:
c) as medidas de localização;
d) as medidas de dispersão;
e) o percentil 90.
6. A tabela seguinte mostra a distribuição da população residente em Portugal, no ano de 2011, segundo o grupo etário (valores arredondados aos milhares): $$ \newcommand\T{\Rule{0pt}{0.25em}} \begin{array}{ |c| c |} \hline Grupo\;etário & População \\ (anos) & (milhares)\\ \hline 0 - 9 & 1008 \\ 10 - 19 & 1130 \\ 20 - 29 & 1238 \\ 30 - 39 & 1598 \\ 40 - 49 & 1543 \\ 50 - 59 & 1400 \\ 60 - 69 & 1186 \\ 70 - 79 & 926 \\ \ge 80 & 532 \\ \hline Total & 10561 \\ \hline \end{array} $$ Fonte: Instituto Nacional de Estatística, Censos - Resultados definitivos. Portugal - 2011
a) Calcule as medidas de localização;
b) Apresente um Histograma de frequências absolutas;
c) Calcule a percentagem de portugueses com idade superior a 65 anos;
d) Calcule o percentil 5.
Resolução em EXCEL
7. Com o objetivo de analisar a distribuição remuneratória presente numa empresa industrial foram recolhidos os salários mensais, em euros, dos 25 trabalhadores:
$$ \newcommand\T{\Rule{0pt}{0.25em}} \begin{array}{ |c| c |c|c|c|} \hline 350 & 450 & 600 & 350& 350 \\ 350 & 450 & 550 & 1500&350 \\ 350 & 450 & 800 & 600 &630 \\ 380 & 490 & 340 & 360& 370\\ 650 & 590 & 390 & 500 & 1250 \\ \hline \end{array} $$ Empregando as medidas descritivas que achar mais convenientes, caracterize os salários dos trabalhadores desta empresa.
8. Durante o período compreendido entre Janeiro de 1991 e Dezembro de 1993, foram registadas as vendas de veículos ligeiros de passageiros e mistos, para os concelhos de Portimão e Faro. O quadro seguinte mostra as unidades vendidas, durante este período de tempo, de forma ordenada.
$$ \begin{array}{ |c c | c c|} \hline Portimão & & Faro & \\ \hline 46 & 90&80&219\\ \hline 59 & 90&84&224 \\ \hline 66 & 93&87&225 \\ \hline 66&99&92&227 \\ \hline 67&106&126&227 \\ \hline 71&107&130&233 \\ \hline 73&111&136&234 \\ \hline 73&114&142&234 \\ \hline 75&116&143&245 \\ \hline 78&117&157&245 \\ \hline 81&122&159&245 \\ \hline 82&125&167&254 \\ \hline 83&145&178&256 \\ \hline 85&179&178&269 \\ \hline 85&190&185&289 \\ \hline 85&205&187&290 \\ \hline 88&266&190&302 \\ \hline 88&268&190&307 \\ \hline \end{array} $$ Para as vendas nos dois concelhos:
a) Calcule as medidas de localização e dispersão;
b) Apresente o gráfico extremos-quartis;
c) Construa a distribuição de frequências;
d) Represente o Histograma.
10. Após examinar os registos das contas de uma empresa, o auditor formou uma amostra de 20 contas não pagas, com os seguintes valores em milhares de euros: $$ \newcommand\T{\Rule{0pt}{0.25em}} \begin{array}{ |c|c|c|c|c|c|c|c|c|c|} \hline 4 & 18 & 11 & 7& 7 & 10 &5&33&9&12\\ 3&11&10&6&26&37&15&18&10&21 \\ \hline \end{array} $$ a) Calcule a média, a mediana e a moda.
b) Se o total de contas por pagar for 350, utilize a média para estimar o montante total das dívidas à empresa
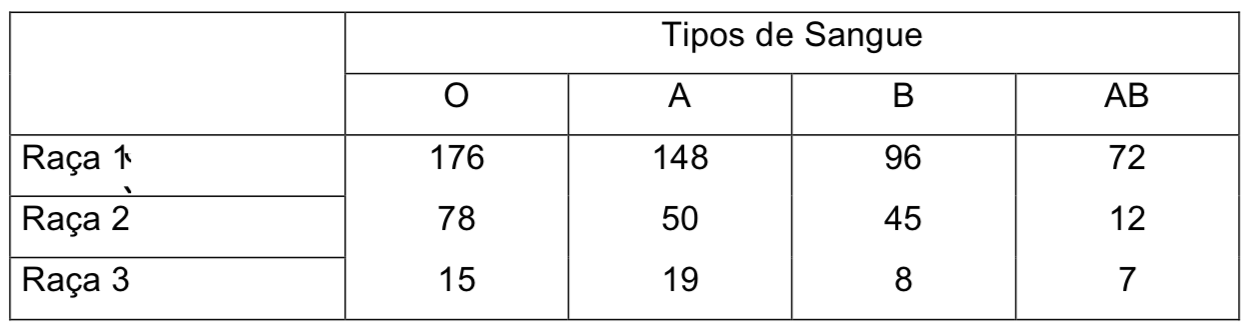
11. O quadro seguinte é baseado num estudo que relaciona a raça com o tipo de sangue.
a) Calcule o qui-quadrado.
b) Calcule o coeficiente de contingência.
c) Interprete os resultados obtidos.
12.. O produto interno bruto português, a preços constantes de 1995, e o respectivo índice de preços, evoluíram da seguinte forma entre 1995 e 2013:
| ||||
b) Calcule a taxa de variação média.
c) Ajuste uma tendência linear.
13. Considere a série cronológica seguinte: $$ \newcommand\T{\Rule{0pt}{0.5em}} \begin{array}{|c|c|c|c|c|c|} \hline \text{Anos}& \text{1985} & \text{1986} & \text{1987} & \text{1988} & \text{1989} \\\hline \text{Exportações (preços correntes} &120 & 140 & 170 & 205 & 250 \\\hline \text{Índice de preços (1985=100)} &100 & 115 & 130 & 150 & 190 \\\hline \end{array} $$ Indique o valor das exportações a preços constantes de 1988.
14. Considere os seguintes valores referentes ao PIB (Produto Interno Bruto) do País A. $$ \newcommand\T{\Rule{0pt}{0.5em}} \begin{array}{|c|c|c|c|c|c|c|} \hline \text{Anos}& \text{1985} & \text{1986} & \text{1987} & \text{1988} & \text{1989} & \text{1990} \\\hline \text{Preços correntes} &23124 & 27052 & 29481 & 33420 & 38903 & 49041 \\\hline \text{Preços constantes (1990)} &46398 & 46974 & 46193 & 47259 & 48278 & 49041 \\\hline \end{array} $$ Apresente uma série de preços constantes com base em 1985.
15. A tabela seguinte apresenta os salários de um trabalhador (em u.m.) ao longo de 8 anos: $$ \newcommand\T{\Rule{0pt}{0.5em}} \begin{array}{|c|c|c|c|c|c|c|} \hline \text{Anos}& \text{2000} & \text{2001} & \text{2002} & \text{2003} & \text{2004} & \text{2005}& \text{2006}& \text{2007} \\\hline \text{Salário} &6000 & 6000&6800 & 7000& 7700& 7800& 8400 &9000 \\\hline \end{array} $$ a) Deflacione os salários de modo a obter uma série de valores representativos dos salários reais utilizando o IPC com base no ano 2000.
$$ \newcommand\T{\Rule{0pt}{0.5em}} \begin{array}{|c|c|c|c|c|c|c|} \hline \text{Anos}& \text{2000} & \text{2001} & \text{2002} & \text{2003} & \text{2004} & \text{2005}& \text{2006}& \text{2007} \\\hline \text{IPC} &118 & 122&127 & 131& 143& 157& 172 &190 \\\hline \end{array} $$ b) Analise os resultados obtidos.
16. O preço da matéria prima X, tem registado nos últimos anos a evolução representada no seguinte quadro: $$ \newcommand\T{\Rule{0pt}{0.5em}} \begin{array}{|c|c|c|c|c|c|c|} \hline \text{Anos}& \text{1985} & \text{1986} & \text{1987} & \text{1988} & \text{1991} \\\hline \text{Preços correntes (euros)} &2000 & 2040 & 2125 & 2712 & 4645 \\\hline \text{Índices de Preços (1985=100)} &100 & 103.5 & 105.2 & & \\\hline \text{Índices de Preços (1988=100)} & & &93.2 & 100.0 &125.0 \\\hline \end{array} $$ (Nota: em relação aos anos de 1989 e 1990 não existem dados disponíveis)
Para o período temporal em foco, construa uma série de preços constantes de 1991 para a matéria prima X.
Solução
17. A produção de uma fábrica é composta por três bens distintos. As quantidades produzidas (em toneladas) e os preços (em euros) praticados ao longo de quatro anos foram registados no quadro seguinte. $$ \newcommand\T{\Rule{0pt}{0.5em}} \begin{array}{|l|cc|cc|cc|cc|} \hline Anos & \text{2015(ano base)} & & \text{2016} & & \text{2017} & & \text{2018} & \\ Bens & Preço & Quantidade & Preço & Quantidade & Preço & Quantidade & Preço & Quantidade \\\hline \text{Bem A} & 5 & 10 & 6 & 12 & 7 & 9 & 8 & 10 \\ \text{Bem B} & 10 & 6 & 8 & 7 & 8 & 6 & 11 & 8 \\ \text{Bem C} & 7 & 8 & 7 & 8 & 8 & 9 & 5 & 10 \\ \hline \end{array} $$ a) Podemos afirmar que a evolução do valor da produção, a preços correntes, foi sempre positiva ao longo destes quatro anos?
b) Calcule o índice de preços de Paasches;
c) Utilizando o resultado calculado na alínea anterior obtenha a série do valor da produção a preços constantes de 2015;
d) Obtenha um ínice de quantidades;
e) Avalie a evolução da produção ao longo destes quatro anos.