De uma forma geral uma variável aleatória corresponde a uma regra de atribuição de valores numéricos a resultados de uma determinada experiência. Por exemplo, se lançarmos uma moeda 10 vezes, então o número de ‘caras’ que poderemos obter com essa experiência corresponde a \(\Omega =\{0, 1, 2, ..., 10\}\).
Portanto, a primeira razão para definirmos uma variável aleatória resulta da necessidade de substituirmos o espaço de resultados intrínseco à experiência por um outro composto por valores numéricos. Podemos assim responder a questões como o nº de caras expectáveis, ou a probabilidade de saírem 5 caras, ou menos de 5 caras?
Neste contexto, a variável aleatória pode ser discreta ou contínua. No caso discreto a variável aleatória pode assumir um número finito ou um número infinito, mas perfeitamente identificável e contável, de valores possíveis. É o caso do lançamento da moeda ao ar, uma vez que, em tese, é sempre possível lançar uma vez mais a moeda, sem qualquer limite, e desse modo o número de 'caras' que se podem obter também não tem limite, contudo, não ter limite não significa que não se possa contar todas as possibilidades. Seja qual for o número de possibilidades discretas inerentes à experiência aleatória é possível atribuir uma probabilidade não nula a cada um desses resultados possíveis.
Teoremas
(1) \(0 \leq F(x) \leq 1\)
(2) \(F(x)\) é não decrescente \( \Delta x > 0 ⇒ F(x) ≤ F(x+\Delta x)\)
(3) Dado \(x_1\) e \(x_2\) e \(x_2 > x_1\) tem-se \( P(x \lt X \leq x_2) = F(x_2) - F(x_1) \)
\( (1) P(X ≤ x) = F(x)\) (por definição)
(2) \(P(X \lt x) = P(X \leq x) - P(X = x)\)
(3) \(P(X \gt x) = 1- P(X \leq x) = 1 - F(x)\)
(4) \(P(X \leq x) = 1- P(X \gt x)\)
(5) \(P(x_1 \lt X \leq x_2) = F(x_2) - F(x_1)\)
(6) \(P(x_1 \lt X \lt x_2) = P(x_1 \lt X \leq x_2) - P(X = x_2)\)
(7) \(P(x_1 \leq X \lt x_2) = P(x_1 \lt X \lt x_2) + P(X = x_1)\)
(8) \(P(x_1 \leq X \leq x_2) = P(x_1 \lt X \leq x_2) + P(X = x_1)\)
\(f(x) \geq 0 \)
\(\sum f(x_i) =1\)
\( F(x)=P(X\leq x) \Leftrightarrow \sum_{a_i \lt x}f(a_i) \).
\(f(x) = \left(\!\begin{array}{c} n \\ x\end{array}\!\right) p^x q^{n-x}\)
é uma função probabilidade adequada a representar esta experiência aleatória. Neste caso, se repetirmos o lançamento da moeda 6 vezes então n = 6 e o acontecimento saída de cara tem um espaço de resultados discreto entre 0 e 6, ou seja, os valores possíveis da variável aleatória X são \( (x_1=0, x_2=1, x_3=2, x_4=3, x_5=4, x_6=5, x_7=6) \).
Assim, se lançarmos 6 vezes uma moeda ao ar a probabilidade de não sair nenhuma cara será
\( x = 0 \Rightarrow P(X=0) = f(0) = \left(\!\begin{array}{c} 6 \\ 0\end{array}\!\right) \left(\frac{1}{2}\right)^0 \left(\frac{1}{2}\right)^{6-0} = 0.016\).
A probabilidade de sair apenas uma cara será
\( x = 1 \Rightarrow P(X=1) = f(1) = \left(\!\begin{array}{c} 6 \\ 1\end{array}\!\right) \left(\frac{1}{2}\right)^1 \left(\frac{1}{2}\right)^{6-1} = 0.094\).
E assim sucessivamente,
\( x = 2 \Rightarrow P(X=2) = f(2) = \left(\!\begin{array}{c} 6 \\ 2\end{array}\!\right) \left(\frac{1}{2}\right)^2 \left(\frac{1}{2}\right)^{6-2} = 0.234\);
\( x = 3 \Rightarrow P(X=3) = f(3) = \left(\!\begin{array}{c} 6 \\ 3\end{array}\!\right) \left(\frac{1}{2}\right)^3 \left(\frac{1}{2}\right)^{6-3} = 0.313\);
\( x = 4 \Rightarrow P(X=4) = f(4) = \left(\!\begin{array}{c} 6 \\ 4\end{array}\!\right) \left(\frac{1}{2}\right)^4 \left(\frac{1}{2}\right)^{6-4} = 0.234\);
\( x = 5 \Rightarrow P(X=5) = f(5) = \left(\!\begin{array}{c} 6 \\ 5\end{array}\!\right) \left(\frac{1}{2}\right)^5 \left(\frac{1}{2}\right)^{6-5} = 0.094\);
\( x = 6 \Rightarrow P(X=6) = f(6) = \left(\!\begin{array}{c} 6 \\ 6\end{array}\!\right) \left(\frac{1}{2}\right)^6 \left(\frac{1}{2}\right)^{6-6} = 0.016\).
Em termos gráficos
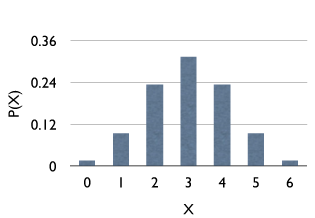
$$ \sum_{i=0}^6 P(X=x_i) =1 $$.
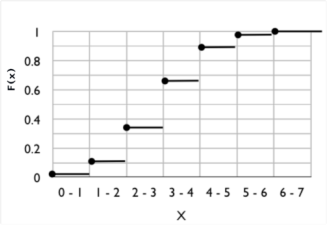
$$F(x) = \left\{ \begin{array}{l l l l l l l l} 0 & x \lt 0 \\ 0.016 & 0 \leq x \lt 1 \\ 0.109 & 1 \leq x \lt 2 \\ 0.344 & 2 \leq x \lt 3 \\ 0.656 & 3 \leq x \lt 4 \\ 0.891 & 4 \leq x \lt 5 \\ 0.984 & 5 \leq x \lt 6 \\ 1 & x \geq 6 \end{array} \right. $$ e a sua representação gráfica será a seguinte
e como
$$P(X=x_1)=P(X=x_2)=0$$ então
$$ \fbox{$\int_{x_1}^{x_2} f(x)\,\mathrm{d}x = P(x_1 \lt X \leq x_2) = P(x_1 \leq X \lt x_2) = P(x_1 \leq X \leq x_2)$}$$.
A probabilidade de uma componente escolhida ao acaso:
a) Durar menos de 4000 horas;
$$P(X \lt 4 )=\int_{0}^{4} 0.1e^{-0.1x}\,\mathrm{d}x = \begin{bmatrix} -e^{-0.1x} \end{bmatrix}_0^4 = -e^{-0.4}+1 \approx 0.33$$ b) Durar entre 5000 e 10000 horas.
$$P(5 \lt X \lt 10 )=\int_{5}^{10} 0.1e^{-0.1x}\,\mathrm{d}x = \begin{bmatrix} -e^{-0.1x} \end{bmatrix}_{5}^{10} = -e^{-1}+e^{-0.5} \approx 0.24$$ Da mesma forma podemos calcular a função distribuição
$$ F(x) = \int_{0}^{x} 0.1e^{-0.1u}\,\mathrm{d}u = \begin{bmatrix} -e^{-0.1u} \end{bmatrix}_{0}^{x} = 1-e^{-0.1x} $$ e portanto
$$ P(X \lt 4 )=F(4) =1-e^{-0.4} \approx 0.33 $$
Para variáveis discretas o valor esperado é dado por $$ E(X)= \sum_{i=1}^{n}x_i f(x_i) = \sum_{i=1}^{n}x_i P(X = x_i)$$ correspondendo à média aritmética dos diferentes valores de X ponderados pelas probabilidades respectivas.
Para variáveis contínuas teremos
\( E(X)= \int_{-\infty}^{+\infty}x f(x)dx \) ou se \(X \in [a,b]\) então \(E(X)= \int_{a}^{b}x f(x)dx\)
1. \(E(c) = c\);
2. \(E(cX) = cE(X)\);
3. \(E(X+Y) = E(X)+E(Y)\);
4. Se X e Y independentes \(E(XY) = E(X)E(Y)\);
5. \(E(\sum X_i) = \sum E(X_i)\);
Para variáveis discretas a variância é dada por
$$ V(X)= E(X - E(X))^2 = \sum_{i=1}^{n}(x_i-E(X))^2 f(x_i) $$ e para variáveis contínuas
$$ V(X)= E(X - E(X))^2 = \int_{a}^{b}(x-E(X))^2 f(x)dx $$. E portanto o desvio padrão \( \sigma = \sqrt{V(X)}\).
1. \(V(c) = 0 \)
2. \(V(X+c) = V(X)\)
3. \(V(cX) = c^2V(X)\)
4. \(V(X + Y) = V(X)+V(Y)\) Se X e Y independentes
Portanto, a primeira razão para definirmos uma variável aleatória resulta da necessidade de substituirmos o espaço de resultados intrínseco à experiência por um outro composto por valores numéricos. Podemos assim responder a questões como o nº de caras expectáveis, ou a probabilidade de saírem 5 caras, ou menos de 5 caras?
Neste contexto, a variável aleatória pode ser discreta ou contínua. No caso discreto a variável aleatória pode assumir um número finito ou um número infinito, mas perfeitamente identificável e contável, de valores possíveis. É o caso do lançamento da moeda ao ar, uma vez que, em tese, é sempre possível lançar uma vez mais a moeda, sem qualquer limite, e desse modo o número de 'caras' que se podem obter também não tem limite, contudo, não ter limite não significa que não se possa contar todas as possibilidades. Seja qual for o número de possibilidades discretas inerentes à experiência aleatória é possível atribuir uma probabilidade não nula a cada um desses resultados possíveis.
A função distribuição , \(F(x)=P(X\leq x)\), dá por simples substituição, \(x=x_o\), a probabilidade \(F(x_o)\) de X assumir valor inferior ou igual a um dado número real \(x_o\).
Teoremas
(1) \(0 \leq F(x) \leq 1\)
(2) \(F(x)\) é não decrescente \( \Delta x > 0 ⇒ F(x) ≤ F(x+\Delta x)\)
(3) Dado \(x_1\) e \(x_2\) e \(x_2 > x_1\) tem-se \( P(x \lt X \leq x_2) = F(x_2) - F(x_1) \)
Propriedades
\( (1) P(X ≤ x) = F(x)\) (por definição)
(2) \(P(X \lt x) = P(X \leq x) - P(X = x)\)
(3) \(P(X \gt x) = 1- P(X \leq x) = 1 - F(x)\)
(4) \(P(X \leq x) = 1- P(X \gt x)\)
(5) \(P(x_1 \lt X \leq x_2) = F(x_2) - F(x_1)\)
(6) \(P(x_1 \lt X \lt x_2) = P(x_1 \lt X \leq x_2) - P(X = x_2)\)
(7) \(P(x_1 \leq X \lt x_2) = P(x_1 \lt X \lt x_2) + P(X = x_1)\)
(8) \(P(x_1 \leq X \leq x_2) = P(x_1 \lt X \leq x_2) + P(X = x_1)\)
A função probabilidade ou distribuição de probabilidade \(f(x) = P(X=x)\) caracteriza-se por
\(f(x) \geq 0 \)
\(\sum f(x_i) =1\)
Desta forma
\( F(x)=P(X\leq x) \Leftrightarrow \sum_{a_i \lt x}f(a_i) \).
Consideremos uma vez mais o lançamento de uma moeda ao ar e admitamos que a seguinte função
\(f(x) = \left(\!\begin{array}{c} n \\ x\end{array}\!\right) p^x q^{n-x}\)
é uma função probabilidade adequada a representar esta experiência aleatória. Neste caso, se repetirmos o lançamento da moeda 6 vezes então n = 6 e o acontecimento saída de cara tem um espaço de resultados discreto entre 0 e 6, ou seja, os valores possíveis da variável aleatória X são \( (x_1=0, x_2=1, x_3=2, x_4=3, x_5=4, x_6=5, x_7=6) \).
Assim, se lançarmos 6 vezes uma moeda ao ar a probabilidade de não sair nenhuma cara será
\( x = 0 \Rightarrow P(X=0) = f(0) = \left(\!\begin{array}{c} 6 \\ 0\end{array}\!\right) \left(\frac{1}{2}\right)^0 \left(\frac{1}{2}\right)^{6-0} = 0.016\).
A probabilidade de sair apenas uma cara será
\( x = 1 \Rightarrow P(X=1) = f(1) = \left(\!\begin{array}{c} 6 \\ 1\end{array}\!\right) \left(\frac{1}{2}\right)^1 \left(\frac{1}{2}\right)^{6-1} = 0.094\).
E assim sucessivamente,
\( x = 2 \Rightarrow P(X=2) = f(2) = \left(\!\begin{array}{c} 6 \\ 2\end{array}\!\right) \left(\frac{1}{2}\right)^2 \left(\frac{1}{2}\right)^{6-2} = 0.234\);
\( x = 3 \Rightarrow P(X=3) = f(3) = \left(\!\begin{array}{c} 6 \\ 3\end{array}\!\right) \left(\frac{1}{2}\right)^3 \left(\frac{1}{2}\right)^{6-3} = 0.313\);
\( x = 4 \Rightarrow P(X=4) = f(4) = \left(\!\begin{array}{c} 6 \\ 4\end{array}\!\right) \left(\frac{1}{2}\right)^4 \left(\frac{1}{2}\right)^{6-4} = 0.234\);
\( x = 5 \Rightarrow P(X=5) = f(5) = \left(\!\begin{array}{c} 6 \\ 5\end{array}\!\right) \left(\frac{1}{2}\right)^5 \left(\frac{1}{2}\right)^{6-5} = 0.094\);
\( x = 6 \Rightarrow P(X=6) = f(6) = \left(\!\begin{array}{c} 6 \\ 6\end{array}\!\right) \left(\frac{1}{2}\right)^6 \left(\frac{1}{2}\right)^{6-6} = 0.016\).
Em termos gráficos

E portanto
$$ \sum_{i=0}^6 P(X=x_i) =1 $$.
A função distribuição associada a esta experiência é dada por
$$F(x) = \left\{ \begin{array}{l l l l l l l l} 0 & x \lt 0 \\ 0.016 & 0 \leq x \lt 1 \\ 0.109 & 1 \leq x \lt 2 \\ 0.344 & 2 \leq x \lt 3 \\ 0.656 & 3 \leq x \lt 4 \\ 0.891 & 4 \leq x \lt 5 \\ 0.984 & 5 \leq x \lt 6 \\ 1 & x \geq 6 \end{array} \right. $$ e a sua representação gráfica será a seguinte

No caso contínuo a variável aleatória pode assumir uma infinidade de valores em qualquer intervalo [a, b]. Sendo X uma variável aleatória contínua, então $$F(x) = P(X \leq x) \text{ e } P(X = x) = 0$$
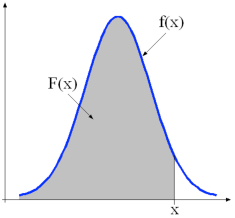 | Considere-se, por exemplo, o intervalo [0, 6] onde a probabilidade de sair o nº 4,567342… é muito próxima de 0. Se X está entre -∞ e +∞, então: $$F(x)= \int_{-\infty}^x f(u)\,\mathrm{d}u$$ $$ \int_{-\infty}^{+\infty} f(x)\,\mathrm{d}x = F(+\infty) - F(-\infty) = 1$$ $$ \int_{x_1}^{x_2} f(x)\,\mathrm{d}x = F(x_2) - F(x_1) = P(x_1 \lt X \leq x_2)$$ |
$$P(X=x_1)=P(X=x_2)=0$$ então
$$ \fbox{$\int_{x_1}^{x_2} f(x)\,\mathrm{d}x = P(x_1 \lt X \leq x_2) = P(x_1 \leq X \lt x_2) = P(x_1 \leq X \leq x_2)$}$$.
Consideremos agora o seguinte exemplo: A duração de vida útil, em milhares de horas, de uma componente de dado aparelho de radar é uma variável aleatória, X, com função densidade
| $$f(x) = \left\{ \begin{array}{l l} 0.1e^{-0.1x} & x \gt 0 \\ 0 & x \leq 0 \end{array} \right. $$ | 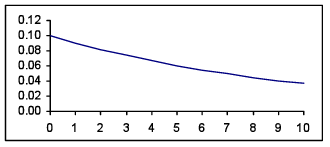 |
a) Durar menos de 4000 horas;
$$P(X \lt 4 )=\int_{0}^{4} 0.1e^{-0.1x}\,\mathrm{d}x = \begin{bmatrix} -e^{-0.1x} \end{bmatrix}_0^4 = -e^{-0.4}+1 \approx 0.33$$ b) Durar entre 5000 e 10000 horas.
$$P(5 \lt X \lt 10 )=\int_{5}^{10} 0.1e^{-0.1x}\,\mathrm{d}x = \begin{bmatrix} -e^{-0.1x} \end{bmatrix}_{5}^{10} = -e^{-1}+e^{-0.5} \approx 0.24$$ Da mesma forma podemos calcular a função distribuição
$$ F(x) = \int_{0}^{x} 0.1e^{-0.1u}\,\mathrm{d}u = \begin{bmatrix} -e^{-0.1u} \end{bmatrix}_{0}^{x} = 1-e^{-0.1x} $$ e portanto
$$ P(X \lt 4 )=F(4) =1-e^{-0.4} \approx 0.33 $$
Valor esperado ou esperança matemática - E(X)
Para variáveis discretas o valor esperado é dado por $$ E(X)= \sum_{i=1}^{n}x_i f(x_i) = \sum_{i=1}^{n}x_i P(X = x_i)$$ correspondendo à média aritmética dos diferentes valores de X ponderados pelas probabilidades respectivas.
Para variáveis contínuas teremos
\( E(X)= \int_{-\infty}^{+\infty}x f(x)dx \) ou se \(X \in [a,b]\) então \(E(X)= \int_{a}^{b}x f(x)dx\)
Propriedades
1. \(E(c) = c\);
2. \(E(cX) = cE(X)\);
3. \(E(X+Y) = E(X)+E(Y)\);
4. Se X e Y independentes \(E(XY) = E(X)E(Y)\);
5. \(E(\sum X_i) = \sum E(X_i)\);
Variância - V(X)
Para variáveis discretas a variância é dada por
$$ V(X)= E(X - E(X))^2 = \sum_{i=1}^{n}(x_i-E(X))^2 f(x_i) $$ e para variáveis contínuas
$$ V(X)= E(X - E(X))^2 = \int_{a}^{b}(x-E(X))^2 f(x)dx $$. E portanto o desvio padrão \( \sigma = \sqrt{V(X)}\).
Propriedades
1. \(V(c) = 0 \)
2. \(V(X+c) = V(X)\)
3. \(V(cX) = c^2V(X)\)
4. \(V(X + Y) = V(X)+V(Y)\) Se X e Y independentes