1.1 História
A evolução das sociedades humanas tem sido no sentido de se tornarem cada vez mais complexas e interdependentes. Um ramo da matemática, conhecido por Estatística, tem acompanhado esta evolução ao longo dos tempos. A necessidade de conhecer para melhor organizar e gerir remonta há milhares de anos. Existem relatos na China que o imperador Yao mandou realizar inventários, mais ou menos regulares, das populações e das lavouras em 2238 a. C.. As civilizações egípcia, grega e romana também utilizaram de forma sistemática registos estatísticos, tendo como objectivos principais a cobrança dos impostos e o cumprimento do serviço militar. É conhecido de todos os Cristãos o recenseamento dos Judeus ordenado pelo Imperador Augusto. Aliás, a etimologia de palavras como estatística, do latim status (estado), ou censo (recenseamento), do latim censu, reflecte esse interesse do Estado (ou da entidade que administra) na recolha de dados quantitativos sobre os indivíduos (os administrados). Em Portugal, foi com D. João III, em 1527, que houve umas das primeiras tentativas para a realização de um recenseamento geral da população e que ficou conhecida pelo “Numeramento de 1527 – 1532” . Tentativa porque segundo Freire, 1905, “o arrolamento se não fez nas vilas de Guimarães e Barcelos porque quem mandava era o Duque de Bragança e o poder real não chegava lá”. Portanto, no desenvolvimento das sociedades humanas, desde muito cedo houve interesse no conhecimento de certas características das populações ainda que com recurso a processos relativamente simples de recolha e processamento dos dados. Esse interesse era de curto prazo e prendia-se com questões imediatas, quantitativas, como a cobrança de impostos ou a constituição de exércitos. Quando esse registo se torna periódico, recolha de dados estatísticos em períodos de tempos regulares, possibilita um conhecimento mais profundo das sociedades do que a simples observação estática. A análise da evolução ao longo do tempo de uma variável, permite determinar tendências para futuro, ou seja, estimar valores para períodos de tempo futuros (previsões). Portanto, o tempo, como em tantos outros aspectos da vida, desempenha, neste contexto, um papel fundamental. Não só a realidade observada muda, como as necessidades de informação mudam ao longo do tempo implicando nesse processo os cientistas e os técnicos no desenvolvimento de novas ferramentas estatísticas.
Medir uma determinada característica, presente numa qualquer população, implica definir o tipo de variável, ou, se quisermos, o tipo de dados a processar no âmbito da análise estatística. Resumimos na tabela seguinte a classificação das variáveis.

- séries (ou sucessões) cronológicas quando as observações se referem a uma única entidade para vários períodos de tempo. A despesa de consumo realizada pelas famílias portuguesas ao longo dos últimos 10 anos e a produção de vinho do porto ao longo dos últimos 20 anos são dois exemplos de séries cronológicas, com periodicidade anual, referentes a dois sectores da economia portuguesa: o das famílias e o do vinho do porto;
- dados seccionais quando as observações se referem a múltiplas entidades para um único período de tempo. Retomando os exemplos anteriores poderíamos agora considerar a despesa de consumo realizada por cada família, residente em Portugal, durante o ano de 2015, ou, a produção de vinho do porto de cada empresa vinícola, com atividade na região demarcada do Douro, em 2015. Neste caso, o período de tempo está fixo (o ano de 2015) e são as entidades (famílias e empresas) que variam;
- dados de painel quando as observações se referem, simultaneamente, a várias entidades e a vários períodos de tempo. É o caso, por exemplo, da despesa de consumo realizada por cada família, residente em Portugal, durante os últimos 10 anos, ou a produção de vinho do porto de cada empresa vinícola, com atividade na região demarcada do Douro, durante os últimos 20 anos.
- se o estudo supõe a destruição ou o consumo do bem (por exemplo os controlos de qualidade de produtos industriais ou agrícolas);
- se o conjunto da população devido à sua dimensão torna-se inacessível (por exemplo a evolução dos preços num país, ou a poluição da água);
- se o próprio orçamento e tempo previsto para o estudo não permitem o recenseamento.
O recenseamento é, geralmente, uma operação mais custosa e mais demorada do que uma sondagem, mas em contrapartida apresenta, em princípio, resultados mais fiáveis. No entanto, a experiência mostra que uma sondagem bem planeada e executada pode dar resultados igualmente fiáveis. As fontes de perturbação que podem afectar os resultados são duas:
- os erros de amostragem que são devidos ao facto de se inferir resultados de uma amostra para uma população;
- os erros de observação que são devidos a inúmeros factores: respostas falsas ou erradas, mal codificadas, a própria falta de respostas, etc.
Seja qual for o tipo de operação estatística, recenseamento ou inquérito por amostragem, que se pretenda desenvolver existem um conjunto de etapas, fases, que importa considerar.
a) definição de objectivos - torna-se necessário também, nesta fase, definir as nomenclaturas, conceitos e metodologias a utilizar compatíveis com os padrões internacionais, de modo a tornar a informação comparável.
Exemplos: Que definição adoptar para desempregado? Como estudar populações nómadas?
b) Definição da população a inquirir - Explicitar as unidades a inquirir (populações humanas, domínio industrial, etc). Inquérito exaustivo ou inquérito por amostragem.
c) Elaboração dos questionários - O tamanho do questionário deve ser o mais pequeno possível; A ordem e a quantidade de perguntas são factores a ter em consideração; Modo de resposta: entrevista pessoal, entrevista telefónica e correio; Formulação das perguntas:
- questões apresentadas de forma clara e com poucas palavras;
- perguntas fechadas ou abertas.
d) Fase de interrogação (trabalho de campo)
Período de referência.
Período de recolha.
e) Registo e controle de coerência (validação)
Detecção de erros através de testes de coerência (testar se existem pais com idade inferior a 10 anos e reformados com idade inferior a 25). Tratamento de não respostas. f) Exploração dos dados e análise
- aleatórios (probabilísticos);
- empíricos (não probabilísticos).
- Amostragem simples: a população é considerada como um todo;
A evolução das sociedades humanas tem sido no sentido de se tornarem cada vez mais complexas e interdependentes. Um ramo da matemática, conhecido por Estatística, tem acompanhado esta evolução ao longo dos tempos. A necessidade de conhecer para melhor organizar e gerir remonta há milhares de anos. Existem relatos na China que o imperador Yao mandou realizar inventários, mais ou menos regulares, das populações e das lavouras em 2238 a. C.. As civilizações egípcia, grega e romana também utilizaram de forma sistemática registos estatísticos, tendo como objectivos principais a cobrança dos impostos e o cumprimento do serviço militar. É conhecido de todos os Cristãos o recenseamento dos Judeus ordenado pelo Imperador Augusto. Aliás, a etimologia de palavras como estatística, do latim status (estado), ou censo (recenseamento), do latim censu, reflecte esse interesse do Estado (ou da entidade que administra) na recolha de dados quantitativos sobre os indivíduos (os administrados). Em Portugal, foi com D. João III, em 1527, que houve umas das primeiras tentativas para a realização de um recenseamento geral da população e que ficou conhecida pelo “Numeramento de 1527 – 1532” . Tentativa porque segundo Freire, 1905, “o arrolamento se não fez nas vilas de Guimarães e Barcelos porque quem mandava era o Duque de Bragança e o poder real não chegava lá”. Portanto, no desenvolvimento das sociedades humanas, desde muito cedo houve interesse no conhecimento de certas características das populações ainda que com recurso a processos relativamente simples de recolha e processamento dos dados. Esse interesse era de curto prazo e prendia-se com questões imediatas, quantitativas, como a cobrança de impostos ou a constituição de exércitos. Quando esse registo se torna periódico, recolha de dados estatísticos em períodos de tempos regulares, possibilita um conhecimento mais profundo das sociedades do que a simples observação estática. A análise da evolução ao longo do tempo de uma variável, permite determinar tendências para futuro, ou seja, estimar valores para períodos de tempo futuros (previsões). Portanto, o tempo, como em tantos outros aspectos da vida, desempenha, neste contexto, um papel fundamental. Não só a realidade observada muda, como as necessidades de informação mudam ao longo do tempo implicando nesse processo os cientistas e os técnicos no desenvolvimento de novas ferramentas estatísticas.
1.2 Conceitos
Medir uma determinada característica, presente numa qualquer população, implica definir o tipo de variável, ou, se quisermos, o tipo de dados a processar no âmbito da análise estatística. Resumimos na tabela seguinte a classificação das variáveis.

Uma outra forma de distinguir o tipo de dados implica introduzir o fator tempo na análise. Assim, podem distinguir-se três categorias de dados:
- séries (ou sucessões) cronológicas quando as observações se referem a uma única entidade para vários períodos de tempo. A despesa de consumo realizada pelas famílias portuguesas ao longo dos últimos 10 anos e a produção de vinho do porto ao longo dos últimos 20 anos são dois exemplos de séries cronológicas, com periodicidade anual, referentes a dois sectores da economia portuguesa: o das famílias e o do vinho do porto;
- dados seccionais quando as observações se referem a múltiplas entidades para um único período de tempo. Retomando os exemplos anteriores poderíamos agora considerar a despesa de consumo realizada por cada família, residente em Portugal, durante o ano de 2015, ou, a produção de vinho do porto de cada empresa vinícola, com atividade na região demarcada do Douro, em 2015. Neste caso, o período de tempo está fixo (o ano de 2015) e são as entidades (famílias e empresas) que variam;
- dados de painel quando as observações se referem, simultaneamente, a várias entidades e a vários períodos de tempo. É o caso, por exemplo, da despesa de consumo realizada por cada família, residente em Portugal, durante os últimos 10 anos, ou a produção de vinho do porto de cada empresa vinícola, com atividade na região demarcada do Douro, durante os últimos 20 anos.
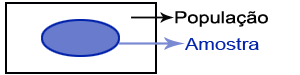
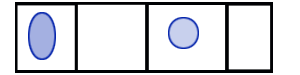
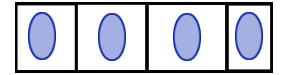
A etapa mais importante no desenvolvimento da estatística levou à diferenciação entre dois conceitos: população versus amostra. É com base nesta diferença que se desenvolveram os dois ramos da estatística clássica: a estatística descritiva e a estatística inferencial. A ideia de elaborar inferências para uma população mais abrangente, a partir e um sub-conjunto dessa população, denominado amostra, apareceu em meados do século XVII. É também verdade que sem a derivação matemática da probabilidade, a inferência estatística estaria muito limitada. Com efeito é a probabilidade que nos permite trabalhar num contexto de incerteza. Na estatística descritiva não existe qualquer incerteza porque o objectivo é sempre a análise, a compreensão, a descrição de uma população (ou universo). Por outro lado, na estatística inferencial existe incerteza porque não temos acesso a toda a informação, apenas podemos aceder a sub-conjuntos dessa informação. Neste contexto, elaborar (inferir) conclusões para uma determinada população com base apenas num conjunto limitado de informação pode levar a conclusões erradas. A operação estatística que permite recolher toda a informação relevante sobre uma população, ou universo, chama-se recenseamento, ou censo. Por outro lado, se apenas for recolhida informação sobre uma amostra a operação denomina-se inquérito por amostragem (ou, por sondagem). Existem muitas situações em que a análise estatística não é possível sem o recurso a uma sondagem:
- se o estudo supõe a destruição ou o consumo do bem (por exemplo os controlos de qualidade de produtos industriais ou agrícolas);
- se o conjunto da população devido à sua dimensão torna-se inacessível (por exemplo a evolução dos preços num país, ou a poluição da água);
- se o próprio orçamento e tempo previsto para o estudo não permitem o recenseamento.
O recenseamento é, geralmente, uma operação mais custosa e mais demorada do que uma sondagem, mas em contrapartida apresenta, em princípio, resultados mais fiáveis. No entanto, a experiência mostra que uma sondagem bem planeada e executada pode dar resultados igualmente fiáveis. As fontes de perturbação que podem afectar os resultados são duas:
- os erros de amostragem que são devidos ao facto de se inferir resultados de uma amostra para uma população;
- os erros de observação que são devidos a inúmeros factores: respostas falsas ou erradas, mal codificadas, a própria falta de respostas, etc.
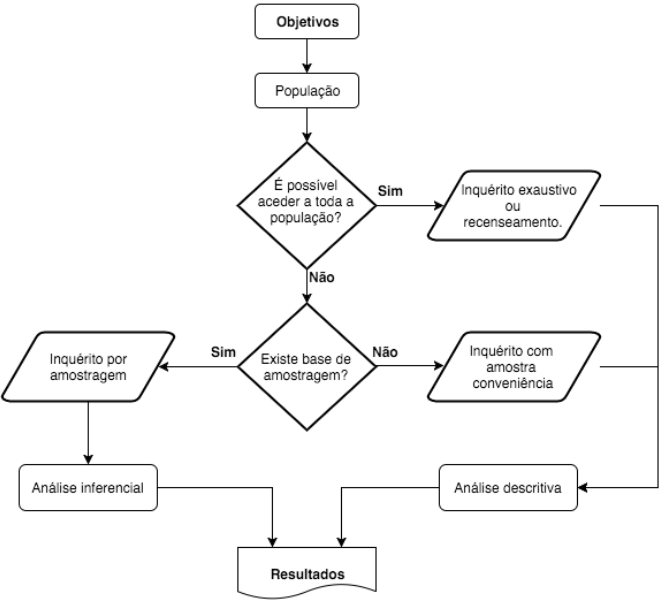
A figura pretende representar o processo de decisão entre a análise descritiva o inferencial.

Seja qual for o tipo de operação estatística, recenseamento ou inquérito por amostragem, que se pretenda desenvolver existem um conjunto de etapas, fases, que importa considerar.
As etapas dos projectos estatísticos:
a) definição de objectivos - torna-se necessário também, nesta fase, definir as nomenclaturas, conceitos e metodologias a utilizar compatíveis com os padrões internacionais, de modo a tornar a informação comparável.
Exemplos: Que definição adoptar para desempregado? Como estudar populações nómadas?
b) Definição da população a inquirir - Explicitar as unidades a inquirir (populações humanas, domínio industrial, etc). Inquérito exaustivo ou inquérito por amostragem.
c) Elaboração dos questionários - O tamanho do questionário deve ser o mais pequeno possível; A ordem e a quantidade de perguntas são factores a ter em consideração; Modo de resposta: entrevista pessoal, entrevista telefónica e correio; Formulação das perguntas:
- questões apresentadas de forma clara e com poucas palavras;
- perguntas fechadas ou abertas.
d) Fase de interrogação (trabalho de campo)
Período de referência.
Período de recolha.
e) Registo e controle de coerência (validação)
Detecção de erros através de testes de coerência (testar se existem pais com idade inferior a 10 anos e reformados com idade inferior a 25). Tratamento de não respostas. f) Exploração dos dados e análise
Um aspecto fundamental para a fiabilidade dos resultados das sondagens é o processo de amostragem porque geralmente as amostras são uma pequeníssima parte do universo e por conseguinte podem fornecer resultados muito enviesados. Os métodos de amostragem (que permitem seleccionar amostras) dividem-se em:
- aleatórios (probabilísticos);
- empíricos (não probabilísticos).
Os métodos empíricos não necessitam de uma base de sondagem, mas podem tirar partido de informações conhecidas a priori e com base nisso construir amostras de conveniência. Neste caso a vantagem é a simplicidade enquanto a desvantagem é a impossibilidade de medir a precisão dos resultados. Nos métodos aleatórios todos os elementos do universo têm uma probabilidade não nula e conhecida de pertencerem à amostra. Esta imposição implica por isso a existência de uma base de sondagem que contenha todas as unidades estatísticas do universo. Ou seja, para seleccionar uma amostra aleatória simples (onde todos os elementos do universo têm a mesma probabilidade de pertencerem a essa amostra) é necessário ter uma lista (base de sondagem) com a identificação de todos os elementos que constituem o universo. Os planos de tiragem, de selecção dos elementos do universo para a amostra, podem ser simples ou a vários níveis:
- Amostragem simples: a população é considerada como um todo;

- Amostragem a vários níveis: a população é dividida em vários subconjuntos, designados de unidades primárias. Existem várias possibilidades, as mais conhecidas são: A amostragem a dois níveis - extrai-se uma amostra de duas unidades primárias e nestas são seleccionadas unidades secundárias.

- A amostragem estratificada - é extraída uma amostra de todas as unidades primárias.

- Amostragem por cachos - extrai-se uma amostra de unidades primárias que se explora totalmente (exemplo: inquirição de todas as pessoas da mesma família)
