Se observarmos para n indivíduos duas quaisquer variáveis X e Y teremos então n pares \((x_i;y_i)\) provenientes dos dois vectores \(\bf x\) e \(\bf y\) de \(\mathbb{R^n}\):
$$\textbf{x}=\begin{bmatrix} x_1 \\x_2 \\...\\x_n \end{bmatrix} \; \; \textbf{y}=\begin{bmatrix} y_1 \\y_2 \\...\\y_n \end{bmatrix}$$
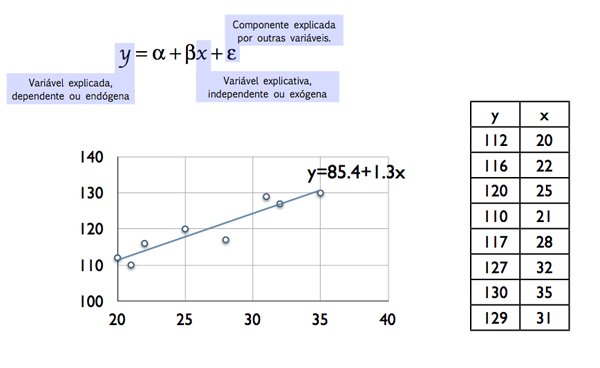 Figura 1.
Figura 1.
Para analisar a relação entre X e Y podemos representar cada observação como um ponto de coordenadas \((x_i, y_i)\) num referencial cartesiano. A nuvem de pontos obtida pode assumir diferentes configurações reveladoras do tipo relação que existirá entre as duas variáveis. Na figura seguinte são apresentadas quatro possibilidades diferentes.
| Ausência de correlação | Correlação linear positiva |
| Correlação linear negativa | Correlação não linear |
O coeficiente de correlação mede o carácter mais ou menos linear da nuvem de pontos e \(-1 \leq r \leq +1\). $$r=\frac{N\sum\limits_{i=1}^Nx_{i}y_{i}-\sum\limits_{i=1}^Nx_{i}\sum\limits_{i=1}^Ny_{i}}{\sqrt{N\sum\limits_{i=1}^Nx_{i}^{2}-(\sum\limits_{i=1}^Nx_{i})^2}\sqrt{N\sum\limits_{i=1}^Ny_{i}^{2}-(\sum\limits_{i=1}^Ny_{i})^2}} $$
Portanto, um valor absoluto próximo de 1 significa que a relação entre X e Y pode ser explicada através da equação de uma recta. Ou seja, cada observação de Y, a variável dependente ou endógena, é explicada pela observação \(x_i\) de X, a variável independente ou exógena, através de uma relação linear do tipo \(y_i=\alpha + \beta x_i+\varepsilon_i\). Representando \(\varepsilon _i \) o desvio (o erro) entre o valor estimado e o observado \(\varepsilon_i = y_i-(\alpha + \beta x_i)= y_i-\hat{y}_i\). Considere-se o exemplo apresentado na figura 1 utilizando uma amostra de 8 observações (n=8):
Figura 1.
 Figura 1.
Figura 1.
| Export to: |
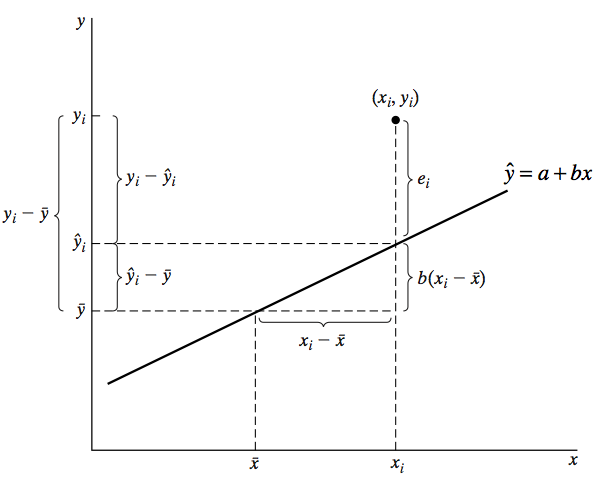
Neste caso, como na generalidade das situações, a nuvem de pontos não representa uma situação completamente linear, existirão sempre desvios entre os valores observados e os pontos de qualquer recta traçada naquele plano. Se minimizarmos a soma dos quadrados dos desvios é possível determinar uma equação da recta que torna \(\sum \limits_{i=1}^{n} \varepsilon_i =0\). A esta concretização (estimativa) de \(\alpha\) e \(\beta\), com base nestas 8 observações, denominaremos a e b, respectivamente. $$b=\frac{N\sum\limits_{i=1}^Nx_{i}y_{i}-\sum\limits_{i=1}^Nx_{i}\sum\limits_{i=1}^Ny_{i}}{N\sum\limits_{i=1}^Nx_{i}^{2}-(\sum\limits_{i=1}^Nx_{i})^2} $$ $$a=\bar{y}-b\bar{x}$$ Portanto, nesta situação concreta, \(\hat{y}_i =85.4+1.3x_i\), significa que a variação de y por cada acréscimo unitário de x será de +1.3. Assim, os erros estimados serão dados por \(e_i = y_i-(85.4+1.3x_i)\). Consideremos agora, para analisar um pouco mais da qualidade presente nesta relação linear, a figura 2 que apresenta para um único valor de \(x_i\) a observação \(y_i\) e a sua estimativa \(\hat{y}_i\).
Figura 2.

A generalização da distância \((y_i-\bar{y}_i)=(y_i-\hat{y}_i)+(\hat{y}_i-\bar{y}_i)\) permite escrever $$\sum \limits_{i=1}^{n} (y_i-\bar{y}_i)^2=\sum \limits_{i=1}^{n}(y_i-\hat{y}_i)^2+\sum \limits_{i=1}^{n}(\hat{y}_i-\bar{y}_i)^2$$ ou SQT = SQE+SQR, onde SQT significa a soma dos quadrados totais, SQE a soma dos quadrados dos erros e SQR a soma dos quadrados explicados plea regressão. Dividindo ambos os termos por n, podemos agora expressar a mesma relação através das variâncias. $$\sum \limits_{i=1}^{n} \frac{(y_i-\bar{y}_i)^2}{n}=\sum \limits_{i=1}^{n} \frac{(y_i-\hat{y}_i)^2}{n}+\sum \limits_{i=1}^{n}\frac{(\hat{y}_i-\bar{y}_i)^2}{n}$$ ou $$S_y^2=S_e^2+S_{\hat{y}}^2$$ Medindo a variabilidade explicada pelo modelo de regressão linear, \(S_{\hat{y}}^2\), em função da variabilidade de y, \(S_y^2\), podemos identificar uma estatística que avalia a qualidade do modelo: o coeficiente de determinação, \(R^2\). $$R^2 = \frac{S_{\hat{y}}^2}{S_y^2} = 1- \frac{S_e^2}{S_y^2} = \frac{SQR}{SQT}=1-\frac{SQE}{SQT}$$ Que representa a percentagem da variabilidade de y explicada pelo modelo de regressão e \(0\leq R^2\leq 1\).