Tabelas de contingência.
Sejam X e Y duas variáveis qualitativas com r e s modalidades, respectivamente. Se utilizarmos uma tabela para estruturar a apresentação dos dados teremos uma tabela de contingência com r linhas e s colunas (veja-se a tabela 1).
Consideremos uma vez mais a turma de 30 alunos do nosso curso de informática divididos agora também por género: 0 - feminino e 1 - masculino. A distribuição cruzada dos alunos pelas modalidades das duas variáveis é apresentada na tabela 2.


1. o coeficiente de contingência de K. Pearson -
Tabela 1.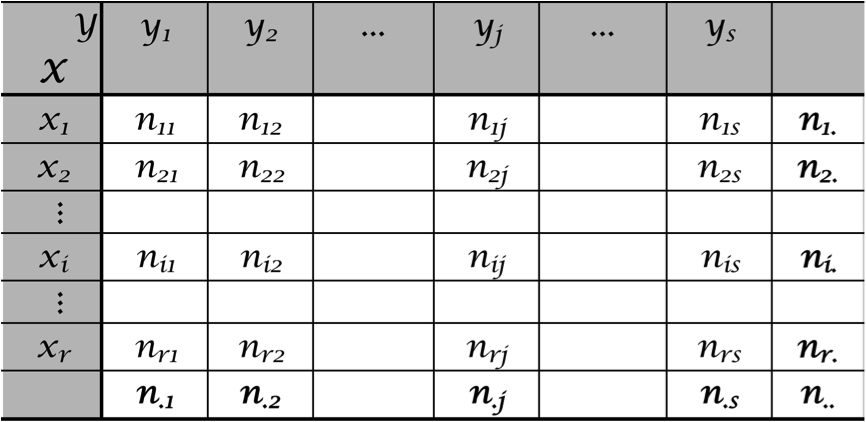
Onde Representando o total em linha e o total em coluna. Neste sentido, o total de indivíduos que constituem esta população (N) é neste caso representado por , sendo |
Tabela 2.

Neste contexto, quando entramos na análise bivariada e cruzamos informação relativa a duas variáveis, podemos responder a outro tipo de questões. Por exemplo, investigar se as duas variáveis estarão ou não relacionadas (associadas). Poderemos, ou não, associar certas modalidades da variável X com determinadas modalidades da variável Y? Ou seja, neste universo de 30 alunos, existirá uma associação entre o resultado da avaliação e o género? O género feminino, ou masculino, estará associado com algum dos resultados (excluído, admitido ou dispensado)? Para responder a esta questão importa, em primeiro lugar, notar que a partir de uma tabela de contingência podem ser realizadas duas leituras consoante a variável que se priviligie: a leitura em linha ou a leitura em coluna. Se a opção for a linha então as frequências condicionais que importam são calculadas por , enquanto no caso da coluna será . Assim, se pretendermos saber como se distribuem as classificações por rapazes e raparigas, então teremos dos alunos excluídos são raparigas, enquanto apenas são rapazes. Nos alunos admitidos são raparigas (44,4%) e são rapazes (55,6%). Nos dispensados as proporções para raparigas e rapazes alteram-se significativamente para 20% e 80%, respectivamente. Por outro lado, se pretendermos saber as classificações obtidas por cada género, então teremos das raparigas foram excluídas (42%), foram admitidas (33%) e foram dispensadas (25%). Nos rapazes teremos então 5,6% de excluídos, 27,8% admitidos e 66,6% dispensados.
O desvio à independência Se as proporções (as frequências condicionadas) encontradas em todas as linhas forem idênticas,i.e., então podemos dizer que as variáveis X e Y são independentes, uma vez que o conhecimento de X não muda a distribuição condicional de Y. Resultando daqui por soma dos numeradores e denominadores que Portanto, a situação de independência é dada por que representa a frequência esperada (teórica) caso as variáveis sejam independentes. No nosso exemplo a situação de independência, que corresponde à distribuição proporcional dos indivíduos segundo a estrutura em linha ou segundo a estrutura em coluna, é apresentada na tabela 3.
Tabela 3.

Neste sentido, quanto maior forem as diferenças entre e maior tenderá a ser a associação entre X e Y. É geralmente aceite como medida de associação o qui-quadrado - - dado por: Portanto, se então estaremos no caso em que as variáveis são independentes e . No entanto, o problema surge no limite superior a partir do qual possamos estabelecer uma dependência funcional uma vez que ou . Para ultrapassar esta dificuldade diversos coeficientes foram propostos para obter uma medida que varie entre 0 (independência) e 1 (ligação funcional).
1. o coeficiente de contingência de K. Pearson -
2. o coeficiente de Tschuprow -
3. o coeficiente de Cramer -
No exemplo dos alunos teremos então e o que permite afirmar a existência de alguma associação entre género e resultado do exame. Com efeito, comparando as frequências observadas, presentes na tabela 2, e as frequências esperadas, presentes na tabela 3, verifica-se que os alunos do género feminino estarão associados a resultados mais negativos (exclusão) enquanto os alunos masculinos estarão mais associados a resultados positivos (dispensa).